helm.h File Reference

A header-only PID controller based largely on Chapter 10 of Astrom and Murray. More...

Data Structures
struct	helm_state
	Tuning parameters and internal state for an incremental PID controller. More...

Functions
static struct helm_state *	helm_reset (struct helm_state *const h)
	Reset all tuning parameters, but not transient state. More...
static struct helm_state *	helm_approach (struct helm_state *const h)
	Reset any transient state, but not tuning parameters. More...
static double	helm_steady (struct helm_state *const h, const double dt, const double r, const double u, const double v, const double y)
	Find the control signal necessary to steady unsteady process y(t). More...

Detailed Description

A header-only PID controller based largely on Chapter 10 of Astrom and Murray.

This proportional-integral-derivative (PID) controller features

• low pass filtering of the process derivative,
• windup protection,
• automatic reset on actuator saturation,
• anti-kick on setpoint change using "derivative on measurement",
• incremental output for bumpless manual-to-automatic transitions,
• a unified controller gain parameter,
• exposure of all independent physical time scales, and
• the ability to accommodate varying sample rate.

Block diagram for the controller

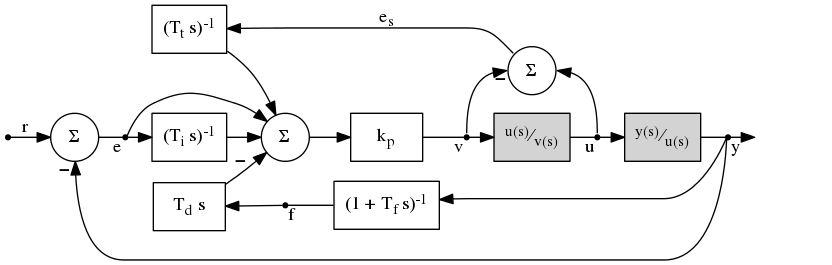
Let \(f\) be a first-order, low-pass filtered version of controlled process output \(y\) governed by

\begin{align} \frac{\mathrm{d}}{\mathrm{d}t} f &= \frac{y - f}{T_f} \end{align}

where \(T_f\) is a filter time scale. Then, in the time domain and expressed in positional form, the control signal \(v\) evolves according to

\begin{align} v(t) &= k_p \, e(t) + k_i \int_0^t e(t) \,\mathrm{d}t + k_t \int_0^t e_s(t) \,\mathrm{d}t - k_d \frac{\mathrm{d}}{\mathrm{d}t} f(t) \\ &= k_p \left[ e(t) + \frac{1}{T_i} \int_0^t e(t) \,\mathrm{d}t + \frac{1}{T_t} \int_0^t e_s(t) \,\mathrm{d}t - T_d \frac{\mathrm{d}}{\mathrm{d}t} f(t) \right] \\ &= k_p \left[ \left(r(t) - y(t)\right) + \frac{1}{T_i} \int_0^t \left(r(t) - y(t)\right) \,\mathrm{d}t + \frac{1}{T_t} \int_0^t \left(u(t) - v(t)\right) \,\mathrm{d}t + \frac{T_d}{T_f}\left(f(t) - y(t)\right) \right] \end{align}

where \(u\) is the actuator position and \(r\) is the desired reference or "setpoint" value. Constants \(T_i\), \(T_t\), and \(T_d\) are the integral, automatic reset, and derivative time scales while \(k_p\) specifies the unified gain. Differentiating one finds the "incremental" form written for continuous time,

\begin{align} \frac{\mathrm{d}}{\mathrm{d}t} v(t) &= k_p \left[ - \frac{\mathrm{d}}{\mathrm{d}t} y(t) + \frac{r(t) - y(t)}{T_i} + \frac{u(t) - v(t)}{T_t} + \frac{T_d}{T_f}\left( \frac{\mathrm{d}}{\mathrm{d}t} f(t) - \frac{\mathrm{d}}{\mathrm{d}t} y(t) \right) \right] . \end{align}

Here, to avoid controller kick on instantaneous reference value changes, we assume \(\frac{\mathrm{d}}{\mathrm{d}t} r(t) = 0\). This assumption is sometimes called "derivative on measurement" in reference to neglecting the non-measured portion of the error derivative \(\frac{\mathrm{d}}{\mathrm{d}t} e(t)\).

Obtaining a discrete time evoluation equation is straightforward. Multiply the above continuous result by the time differential, substitute first order backward differences, and incorporate the low-pass filter in a consistent fashion. One then finds the following:

\begin{align} {\mathrm{d}t}_i &= t_i - t_{i-1} \end{align}

\begin{align} f(t_i) &= \frac{ {\mathrm{d}t}_i\,y(t_i) + T_f\,f(t_{i-1}) } { T_f + {\mathrm{d}t}_i } = \alpha y(t_i) + (1 - \alpha) f_{i-1} \quad\text{with } \alpha=\frac{{\mathrm{d}t}_i}{T_f + {\mathrm{d}t}_i} \end{align}

\begin{align} {\mathrm{d}f}_i &= f(t_i) - f(t_{i-1}) = \alpha\left( y(t_i) - f(t_{i-1}) \right) \end{align}

\begin{align} {\mathrm{d}y}_i &= y(t_i) - y(t_{i-1}) \end{align}

\begin{align} {\mathrm{d}v}_i &= k_p \left[ {\mathrm{d}t}_i \left( \frac{r(t_i) - y(t_i)}{T_i} + \frac{u(t_i) - v(t_i)}{T_t} \right) + \frac{T_d}{T_f}\left( {\mathrm{d}f}_i - {\mathrm{d}y}_i \right) - {\mathrm{d}y}_i \right] \end{align}

where notice \(f(t)\) is nothing but an exponential weighted moving average of \(y(t)\) that permits varying the sampling rate. An implementation needs only to track two pieces of state, namely \(f(t_{i-1})\) and \(y(t_{i-1})\), across time steps.

Sample written with nomenclature from helm_state and helm_steady():

struct helm_state h;

// Set PID parameters from commonly given \c kp, \c ki, \c kt, and \c kd
helm_reset(&h);
h.kp = kp;
h.Td = kd / h.kp;
h.Tf = h.Td / 10;  // Astrom and Murray p.308 suggests 2--20
h.Ti = h.kp / ki;
h.Tt = h.kp / kt;

// Enable automatic control and evolve
helm_approach(&h);
for (int i = 0; i < N; ++i) {
   y  = process(dt, u);
   v += helm_steady(&h, dt, r, u, v, y);
   u  = actuate(dt, v);
}

// Disable controller and evolve
for (int i = 0; i < N; ++i) {  // E
   y  = process(dt, u);
   u  = actuate(dt, v);
}

// Re-enable automatic control and evolve
helm_approach(&h);
for (int i = 0; i < N; ++i) {
   y  = process(dt, u);
   v += helm_steady(&h, dt, r, u, v, y);
   u  = actuate(dt, v);
}

---

Data Structure Documentation

struct helm_state

Tuning parameters and internal state for an incremental PID controller.

Gain kp has units of \(u_0 / y_0\) where \(u_0\) and \(y_0\) are the natural actuator and process observable signals, respectively. Parameter Tt has units of time multiplied by \(u_0 / y_0\). Parameters Td, Tf, and Ti possess units of time. Time units are fixed by the scaling provided in the dt argument to helm_steady().

Data Fields
double	kp	Proportional gain modifying P, I, and D terms.
double	Td	Time scale governing derivative action. Set to zero to disable derivative control.
double	Tf	Time scale filtering process observable for D. Set to infinity to disable observable filtering.
double	Ti	Time scale governing integral action. Set to infinity to disable integral control.
double	Tt	Time scale governing automatic reset. Set to infinity to disable automatic reset.
double	y	Internal tracking of the process observable.
double	f	Internal tracking the filtered process.

Function Documentation

static struct helm_state* helm_reset ( struct helm_state *const  h)

static

Reset all tuning parameters, but not transient state.

Resets gain to one and disables filtering, integral action, and derivative action. Enable those terms by setting their associated time scales.

Parameters

[in,out]

h

Houses tuning parameters to be reset.

Returns

Argument h to permit call chaining.

{
    h->kp = 1;        // Unit gain
    h->Td = 0;        // No derivative action
    h->Tf = INFINITY; // No filtering
    h->Ti = INFINITY; // No integral action
    h->Tt = INFINITY; // No automatic reset
    return h;
}

static struct helm_state* helm_approach ( struct helm_state *const  h)

static

Reset any transient state, but not tuning parameters.

Necessary to achieve bumpless manual-to-automatic transitions before calling to helm_steady() after a period of manual control, including before the first call to helm_steady().

Parameters

[in,out]

h

Houses transient state to be reset.

Returns

Argument h to permit call chaining.

{
    assert(h->Td >= 0);
    assert(h->Tf >  0);
    assert(h->Ti >  0);
    assert(h->Tt >  0);
    h->f = NAN;
    return h;
}

static double helm_steady ( struct helm_state *const  h, const double  dt, const double  r, const double  u, const double  v, const double  y  )

inlinestatic

Find the control signal necessary to steady unsteady process y(t).

Parameters

[in,out]	h	Tuning parameters and state maintained across invocations.
[in]	dt	Time since last samples collected.
[in]	r	Reference value, often called the "setpoint".
[in]	u	Actuator signal currently observed.
[in]	v	Actuator signal currently requested.
[in]	y	Observed process output to drive to r.

Returns

Incremental suggested change to control signal v.

See Also

Overview of helm.h for the discrete evolution equations.

{
    double dv = 0;

    if (!isnan(y)) {                      // Avoid driving blind

        if (isnan(h->f)) {                // Avoid startup kick
            h->y = y;
            h->f = y;
        }

        double a, df, dy;
        a   = dt / (h->Tf + dt);          // Convex combination parameter alpha
        df  = a*(y - h->f);               // Filtered difference for y
        dy  =    y - h->y ;               // Backward difference for y
        dv += (r - y) / h->Ti;            // Action from integral control
        dv += (u - v) / h->Tt;            // Action from automatic reset
        dv *= dt;                         // Scale integral actions by time step
        dv += (h->Td / h->Tf)*(df - dy);  // Action from derivative control
        dv += /*dr=0*/ - dy;              // Action from proporational control
        dv *= h->kp;                      // Scale by unified gain parameter

        h->y  = y;                        // Update observable for next call
        h->f += df;                       // Update filter for next call
    }

    return dv;
}